Les protéines sont les acteurs essentiels de la cellule : catalyseurs, moteurs, lisant et interprétant l’information génétique, coordonnant la réponse aux signaux externes et aux agressions éventuelles. Avec le séquençage de plus de 1 000 génomes au cours de la dernière décennie, nous connaissons la séquence de la totalité des protéines de nombreux organismes, bactéries et eucaryotes [ 1]. Mais, pour la plupart, les structures tridimensionnelles ne sont pas connues. Elles sont pourtant essentielles pour identifier et comprendre la fonction des protéines. En effet, l’expérience a largement démontré que l’agencement tridimensionnel précis des atomes est un facteur essentiel au fonctionnement des protéines comme enzymes ou comme partenaires d’associations spécifiques. C’est pourquoi le « problème du repliement » est plus que jamais à l’ordre du jour : en témoigne la construction récente par IBM d’un superordinateur, Blue Gene, dédié à ce problème. Ce problème classique est peut-être le plus important de la biologie moléculaire : prédire la structure tridimensionnelle d’une protéine à partir de sa séquence d’acides aminés, faisant ainsi le lien entre le gène et la structure.

La prédiction de structure d’une protéine (avec la haute précision nécessaire pour comprendre sa fonction) est difficile pour deux raisons. Premièrement, une protéine possède de nombreux degrés de liberté et une « quasi infinité » de conformations possibles. Si l’on considère des acides aminés individuels, seuls ou dans de très petits peptides, on s’aperçoit que chacun peut occuper de l’ordre de dix conformations différentes [ 2]. Pour une protéine de 100 acides aminés, ce sont donc, au moins potentiellement, 10¹⁰⁰ conformations qui existent pour la chaine polypeptidique… La seconde difficulté provient de la faible stabilité des protéines. Pour dénaturer, ou « déplier », une protéine, l’énergie libre à fournir n’est que d’une dizaine de kilocalories/mole ; soit, pour une petite protéine de mille atomes, environ 0,01 kCal/mole par atome, à comparer avec l’énergie d’agitation thermique moyenne à température ambiante, environ 1 kCal/mole par atome. Ainsi, la structure native, repliée, ne se distingue, par son énergie, que très faiblement des états non natifs, complètement ou partiellement dépliés. Heureusement, nous disposons souvent d’informations partielles sur la protéine, qui permettent de focaliser notre recherche sur un sous-ensemble de structures possibles. C’est le cas quand la séquence de la protéine est assez semblable, ou « homologue », à celle d’une autre protéine dont la structure est connue. Le problème de la prédiction de structure se réduit dans ce cas à une modélisation par homologie.

Le lecteur attentif a peut-être relevé une confusion ici entre « repliement » et « pli ». En effet, en français, le mot repliement désigne tantôt le processus physique par lequel la chaîne polypeptidique atteint sa structure finale repliée, tantôt la structure repliée elle-même, qui devrait plutôt s’appeler le pli. Et la prédiction du processus détaillé de repliement est encore plus difficile que le problème du repliement : en effet, il ne s’agit plus de caractériser seulement la structure finale, repliée, native, mais tout le processus par lequel la protéine néosynthétisée atteint cette structure.

Le problème du repliement et le mécanisme du repliement peuvent tous deux être étudiés par des méthodes de simulation sur ordinateur décrites (brièvement) dans la suite. Nous encourageons ici les lecteurs à participer directement aux recherches dans ce domaine, en installant sur leur ordinateur personnel un économiseur d’écran qui pilote un programme de simulation lorsque leur ordinateur est inutilisé ; ces programmes sont distribués sur Internet à toute personne volontaire [ 3], nous y reviendrons plus loin.

Les problèmes précédents sont liés à un troisième : le problème du repliement inverse. Au lieu de chercher le pli optimal pour une séquence d’acides aminés donnée, il s’agit de trouver la séquence d’acides aminés optimale pour un pli donné. Dans le problème du repliement, nous explorions un vaste espace de conformations. Le problème inverse fait explorer un espace tout autre : celui des séquences. Et nous ramène donc au génome, dont nous étions partis.

Une protéine est un hétéropolymère d’acides aminés ; les acides aminés sont choisis parmi une petite chimiothèque naturelle de vingt composés. Le repliement produit une ségrégation de groupes alcanes au cœur de la protéine et une exposition au solvant des chaînes latérales les plus polaires. Cette ségrégation réduit les zones de contact alcane-eau, qui sont pénalisantes du point de vue thermodynamique : on dit que la structure repliée est stabilisée par l’effet hydrophobe (des groupes alcanes). L’état déplié, quant à lui, est stabilisé par le nombre astronomique de conformations dépliées possibles : ce nombre de conformations se traduit, dans le langage de la thermodynamique, par une grande entropie, favorisant l’état déplié. En pratique, cela signifie que quand la protéine s’écarte fortement de sa structure native, par exemple à la suite d’un choc avec une autre molécule, elle erre parmi les états non natifs pendant un temps considérable, à l’échelle atomique, avant de retrouver la structure native.

Il faut noter que toutes les séquences d’acides aminés ne se replient pas, loin de là, et toutes ne sont pas utilisées dans le répertoire des protéines connues. L’évolution a sélectionné des séquences aux propriétés bien particulières, et ce n’est que très récemment que nous commençons à comprendre ce qui les caractérise. L’exploration des séquences possibles est liée au problème du repliement inverse, auquel nous reviendrons.

Les modèles théoriques les plus importants aujourd’hui s’appuient sur une « mécanique moléculaire » [ 4]. Ils représentent la protéine comme un ensemble de particules sphériques, incompressibles (ou à peu près, les atomes), reliés par des ressorts et portant chacun une charge électrique. Ces charges permettent de représenter le caractère électropositif ou électronégatif des différents groupes chimiques. Les ressorts maintiennent la stéréochimie et la rigidité usuelles des différents groupes : carbones tétraédriques ou plans, liaisons covalentes simples ou doubles. Les molécules du solvant peuvent être décrites de façon analogue. La paramétrisation d’un tel modèle à l’aide de données expérimentales demande quelques dizaines d’années-chercheur. Une fois en place, et malgré sa simplicité, un modèle de mécanique moléculaire bien paramétré est un outil puissant pour examiner le repliement et la stabilité des biomolécules.

La description ci-dessus met en jeu des objets physiques simples, bien connus depuis Coulomb, Laplace ou Newton. Nous pouvons donc écrire l’énergie potentielle de ce « légo moléculaire ». L’énergie potentielle suffit pour déduire les forces entre les particules, et celles-ci déterminent tous les mouvements du système. Les ordinateurs actuels sont capables de résoudre numériquement les équations du mouvement. Martin Karplus, à Harvard, a obtenu ainsi en 1977 la première description détaillée de la dynamique moléculaire d’une protéine (sur une courte échelle de temps, 10^-11 secondes, faute d’ordinateurs assez puissants à l’époque) [ 5]. En effet, cette technique demande des logiciels complexes et des moyens de calcul certains. Les logiciels aujourd’hui standards [ 6] dépassent les 100 000 lignes de code ; ils ont de nombreuses applications, outre le problème du repliement, comme l’étude d’interactions protéine-ligand ou de mécanismes enzymatiques.

Comment la chaine polypeptidique fait-elle pour explorer 10¹⁰⁰ conformations en un temps raisonnable ? C’est le paradoxe de Levinthal (→)

(→) m/s 2005, n° 6-7, p.601.

La réponse est simple, elle ne les explore pas. Certains chemins vers la structure repliée sont nettement plus probables que d’autres, et leur nombre est nettement plus petit que 10¹⁰⁰. C’est ce qui rend possible la simulation du repliement in silico. Les premiers efforts en ce sens datent de 30 ans [ 7]. Plus récemment, de très importants moyens de calcul ont été mis en œuvre. P. Kollman et Y. Duan ont pu utiliser pendant une année entière un superordinateur nouvellement « à la retraite », au centre de calcul de Pittsburgh, aux États-Unis. Ils ont simulé une microseconde de la dynamique d’une petite protéine en solution [ 8], approchant ainsi l’échelle de temps au cours duquel la protéine se replie expérimentalement, soit cinq ordres de grandeur de plus que Karplus en 1977. Ils ont effectivement observé un début de repliement, la protéine passant d’une structure étendue à une structure compacte, ressemblant (d’assez loin) à la structure native expérimentale. Mais la simulation était encore trop courte pour observer une transition claire vers la vraie structure native.

Plus récemment, l’équipe de V. Pande, à Stanford (États-Unis), s’est tourné vers une ressource nouvelle : le calcul distribué, à travers les ordinateurs de milliers de volontaires. La technique fut initiée par des astrophysiciens, avec un programme de traitement d’images destiné à rechercher des traces de vie intelligente dans les images provenant de téléscopes ou de satellites [ 9]. Ce programme, SETI (search for extra-terrestrial intelligence), est piloté par un économiseur d’écran, le tout étant distribué par Internet à toute personne volontaire, dont le PC effectue alors des calculs de traitement d’images quand le propriétaire ne s’en sert pas. Le programme analogue de Pande, Folding@Home, a mobilisé des centaines de milliers de volontaires depuis 2000 [ 10, 11]. Il a permis, et permet encore, des simulations beaucoup plus longues et nombreuses que la microseconde de Kollman et Duan.

Une façon élégante d’accroître encore les performances des simulations est de réduire le nombre de degrés de liberté explicitement représentés. Au lieu d’entourer la protéine de milliers de molécules d’eau « explicites » (Figure 1A), on cherche une représentation implicite de l’eau. L’eau joue un double rôle dans le repliement : les interactions eau-eau sont à la source de l’effet hydrophobe (voir plus haut), et l’eau interagit fortement avec les groupements polaires et ioniques de la protéine, favorisant leur exposition au solvant. Ces deux effets sont reproduits par un modèle très simple, où l’eau est remplacée par un milieu homogène, polarisable : un continuum diélectrique (autre objet physique connu depuis plus d’un siècle). Chose remarquable, cette technique a permis, en 2002, de prédire la structure repliée d’une petite protéine de 20 acides aminés avant la détermination expérimentale de sa structure, publiée quelques semaines plus tard (Figure 1B). 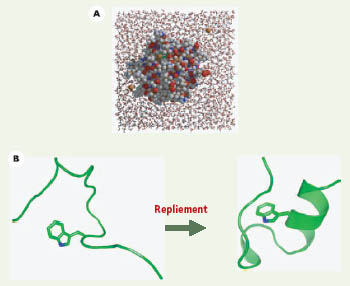L’accord entre la prédiction et l’expérience était excellent [ 12] ; ce fut la première prédiction à haute résolution de la structure d’une protéine à partir de sa seule séquence d’acides aminés. Cette description simplifiée, avec un solvant implicite, a permis ensuite de simuler, sur des ordinateurs de laboratoire, le repliement de plusieurs protéines de petite taille, de 20 à 60 acides aminés. Ainsi, les simulations du processus de repliement ont permis, pour la première fois, de résoudre le problème du repliement.

Figure 1. Représentation explicite et implicite de l’eau et simulation du repliement.A. Molécule de cytochrome c repliée, plongée dans une boîte d’eau : les deux sphères marrons isolées sont des ions chlore. Cette représentation détaillée, avec plusieurs milliers de molécules d’eau explicites, est surtout utilisée pour étudier une protéine déjà repliée. B. Simulation du repliement par représentation implicite de l’eau. Une conformation dénaturée (à gauche) et repliée (à droite) de la petite protéine Trpcage. Son repliement a été simulé avec des représentations implicites, mais aussi explicites du solvant. La structure native (à droite) a été prédite par simulation avant que la structure expérimentale ne soit connue [12] (images préparées avec les programmes Pymol, Molscript et Raster3D [ 19– 21]).

Figure 1. Représentation explicite et implicite de l’eau et simulation du repliement.A. Molécule de cytochrome c repliée, plongée dans une boîte d’eau : les deux sphères marrons isolées sont des ions chlore. Cette représentation détaillée, avec plusieurs milliers de molécules d’eau explicites, est surtout utilisée pour étudier une protéine déjà repliée. B. Simulation du repliement par représentation implicite de l’eau. Une conformation dénaturée (à gauche) et repliée (à droite) de la petite protéine Trpcage. Son repliement a été simulé avec des représentations implicites, mais aussi explicites du solvant. La structure native (à droite) a été prédite par simulation avant que la structure expérimentale ne soit connue [12] (images préparées avec les programmes Pymol, Molscript et Raster3D [ 19– 21]).

Les programmes internationaux de génomique structurale créent une situation nouvelle. Leur objectif est de déterminer la structure de l’ensemble des protéines de plusieurs organismes, choisis pour leur importance biologique ou médicale. Plus exactement, on déterminera expérimentalement un sous-ensemble représentatif de structures : ces structures représentatives sont celles qui sont nécessaires et suffisantes pour modéliser les autres par homologie. En effet, il n’est ni possible, ni vraiment nécessaire de déterminer toutes les structures expérimentalement, du moment que toutes les séquences sont assez proches d’une séquence de structure connue, qui peut servir de base pour une modélisation par homologie [ 13, 14].

Le principe de la modélisation par homologie est simple. Soit P une protéine à modéliser. On identifie d’abord une ou plusieurs protéines (Q, R…) homologues à P, et dont la structure tridimensionnelle est connue. Par alignement des séquences, on identifie les régions les mieux conservées (les plus similaires) parmi toutes ces protéines. Pour ces régions, on adoptera pour la chaîne principale de P le tracé « moyen » des chaînes principales de Q, R,… Pour les régions moins conservées, une modélisation plus coûteuse et compliquée peut être nécessaire. Enfin, on positionne les chaînes latérales de façon à minimiser l’énergie du système. Les deux dernières étapes pourront faire appel, par exemple, à des simulations de dynamique moléculaire et des calculs d’énergie. Ces prédictions font l’objet d’une compétition internationale bisannuelle, appelée CASP (critical assessment of techniques for protein structure prediction) [ 15]. Plusieurs serveurs Web existent, capables d’effectuer ces calculs en ligne.

Ce problème fut posé en 1982 par David Eisenberg [ 16]. Il s’agit d’explorer les séquences compatibles avec un pli donné et d’identifier les plus favorables. Une façon de procéder est d’effectuer des mutations au hasard, partant de la séquence native, et de les accepter ou rejeter selon un critère de stabilité de la protéine mutée. Cela ressemble beaucoup au processus naturel d’évolution, dans lequel on ne prendrait en compte que les mutations ponctuelles, négligeant d’autres événements plus compliqués : épissages erronés, recombinaisons chromosomiques, mutations non-sens. La structure de la protéine mutée doit être prédite après chaque mutation, au cours d’une modélisation par homologie dite « facile » puisque, par définition, la chaîne principale (le pli) n’est pas modifiée. Le changement de stabilité est également estimé après chaque mutation, ce qui suppose de comparer le modèle de la structure repliée avec la (les) structure(s) dépliée(s) ; en effet, une mutation peut être rejetée si elle abaisse trop fortement l’énergie de l’état déplié, même si elle n’a que peu d’effet sur la structure repliée (on pensera au fameux glutamate β6 de l’hémoglobine qui, s’il est muté en valine, ne change pas la stabilité de l’hémoglobine, mais entraîne son aggrégation sous forme de fibres, provoquant l’anémie falciforme).

Un des enjeux actuels est de mener cette exploration de façon exhaustive pour les quelque 3 000 plis connus, ce qui nécessite une puissance de calcul importante. Nous encourageons les lecteurs à rejoindre ces efforts en visitant le site http://boinc.berkeley.edu et en installant sur leur PC un des économiseurs d’écran proposés. Ils participeront ainsi à une cartographie complète de l’espace des séquences compatibles avec les plis connus, un outil qui devrait de révéler puissant pour comprendre l’évolution passée des protéines, mais aussi pour concevoir de nouvelles protéines. En effet, cette stratégie a permis, depuis 2003, d’identifier de nouvelles séquences susceptibles d’adopter un pli choisi à l’avance, et de fonctionner comme enzymes, ou même d’adopter un pli tout à fait nouveau [ 17, 18].

Les simulations ont joué un rôle important, en synergie avec l’expérimentation, pour comprendre le repliement des protéines. La puissance des ordinateurs continue d’augmenter rapidement, et le séquençage des génomes a changé la façon de concevoir la biologie. Aussi, les prochains défis se situent à l’échelle de génomes et d’organismes entiers. Il s’agit de prédire et modéliser la structure de milliers de protéines, dans le cadre de la génomique structurale. Au-delà, il s’agira de dresser une cartographie de toutes les séquences possibles, compatibles avec les quelque 3 000 plis connus. Cette cartographie et cette modélisation éclaireront à la fois l’évolution passée des protéines, leurs fonctions actuelles, et les possibilités d’en concevoir de nouvelles. ◊